
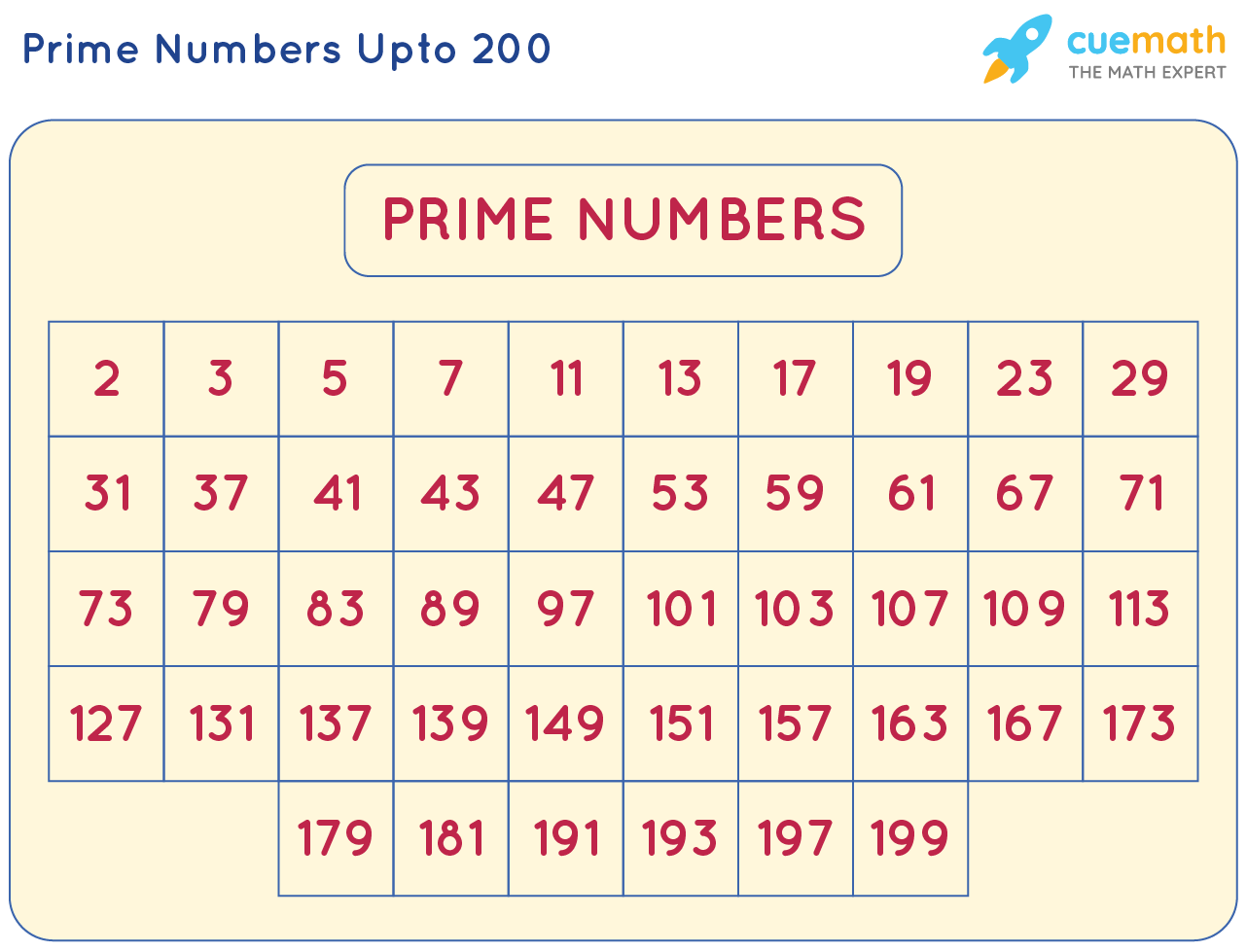
Circle 11 because it is prime, and then cross out all the multiples of 11 except 11 itself.ħ. The most efficient way to find the primes between 101 and 200 is to sieve out any multiples of 2, 3, 5, 7, 11, or 13. You have already found all the primes to 100 and discovered that apart from 2 and 5, all the primes end in 1, 3, 7, or 9. The sieve should give you all the primes found on the hundreds board. Apart from the number 5, all other prime numbers end in 1, 3, 7, or 9.) The numbers shaded on the board below are primes between 1 and 100. 1 has only one factor, itself, so it is not regarded as a prime number.Ĭ.
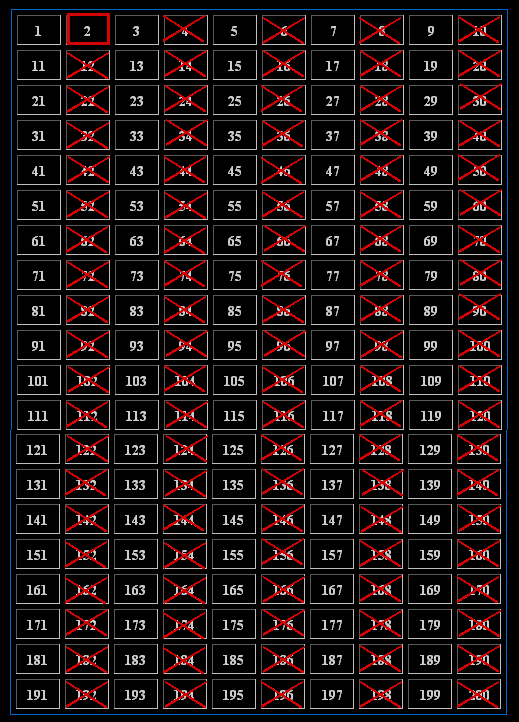
Fat numbers may vary, depending on the factors you choose. But 2 and 3 are also factors of 6, so it is a fat number on the grid.ī. For example, 6 can be shown as a thin number because two of its factors are 6 and 1. Two of their factors are themselves and 1. “Fat” numbers are not primes and have more than 2 factors. Prime numbers only have two factors, themselves and 1, so they are always “thin” numbers. If nothing else, they will be exposed to the passion for maths that many mathematicians feel. An Internet search on emirps, as suggested in the Answers, would be worthwhile, and the students could extend that to searching for information on primes. Have them discuss how they approached finding other 2- and 3-digit emirps. The students can use the primes they found in Investigation One to find some lower value emirps in question 2. In the example illustrated, 1 791 can’t be prime because 3 goes into it 597 times. The number in cell D2 is divisible by the complementary prime in column A, so it cannot be prime itself. If a whole number appears in column B, then The formula checks the number entered in D2 for divisibility by each of the prime numbers in column A. In cell B2, enter the formula =$D$2/A2, then fill down in column B to cell B26 (opposite 97 in column A). To set up this spreadsheet, enter all the prime numbers up to 97 in column A. The number to be tested is entered in cell D2. The spreadsheet shown here can be used to test any number up to 10 000 and see if it is prime. The square root of 10 000 is 100, so each number needs to be divisibility-tested only for prime numbers up to and including 97. Prime numbers up to 10 000 can be found in this way using a spreadsheet program. To do this, all the multiples of 2, 3, 5, 7, 11, 13, … 29 must be eliminated because these numbers are the primes less than 30, which is the square root of 900. You could extend this activity by asking your students to find the primes up to 900. The closest square root to 200 is √196 = 14, so the multiples of 13 are the last that need to be found. Investigation One asks students to work out a way to find primes up to 200. This works because factors exist in pairs and for every prime factor less than the square root, there is a complementary factor greater than the square root. So for the numbers 1 to 100, the multiples of 7 are the last to be eliminated because the next prime (11) is greater than the square root of 100 (10). The sieving process only needs to be continued until the square root of the largest number in the sieve is reached. Because these numbers are multiples, they must be composite. The process involves removing the multiples of 2, then 3, then 5, then 7, and so on. His sieve works by eliminating all the composite numbers, leaving only the prime numbers behind. Eratosthenes, a mathematician of ancient Greece, was famous for calculating the circumference of the Earth. This theorem is the basis of the sieve of Eratosthenes, a method for finding prime numbers, which is explored in Activity Two. This is known as “the fundamental theorem of arithmetic”. The prime factorisation of any composite number is unique no other combination will work. For example, 12 = 2 x 2 x 3 and 15 = 3 x 5.
This means that they can be expressed as the product of primes. Rectangular numbers are also referred to as composite numbers because they are composed of prime factors. A square number has a factor that is used twice (in the case of 16, this factor is 4), but it only appears once on the list of factors for that number. The reason for this is that 16 is a square number, which is a special kind of rectangular number. The dimensions of these rectangles, 2 x 3 and 1 x 6, correspond to the factors of 6, which are.
Two rectangles can be formed from 6 tiles: These activities and investigations are based around prime and non-prime numbers, including square numbers.Īctivity One begins with an illustration that makes a connection between the number of factors that a number has and the number of rectangles that can be formed with that many square tiles.


 0 kommentar(er)
0 kommentar(er)
